USACO Training – Section 1.3 – Transformations
(requires login)
Edit: Sorry I didn’t realise the link to the question required login. Here is a screenshot for the question:
I originally believe that I have understood the question correctly, however, the second testcase contradicts my understanding:
Code:
/*
ID: {my id}
PROG: transform
LANG: C++
*/
#include <iostream>
#include <cstdio>
#include <string>
#include <vector>
using namespace std;
string oriGrid[10], newGrid[10];
bool identical(string* a, string* b, int n);
void rotate90(string* a, int n);
void horizontalReflection(string* a, int n);
int main()
{
freopen("transform.in", "r", stdin);
freopen("transform.out", "w", stdout);
int n;
cin >> n;
for (int i = 0; i < n; ++i) cin >> oriGrid[i];
for (int i = 0; i < n; ++i) cin >> newGrid[i];
rotate90(oriGrid, n);
for (int i = 0; i < 3; ++i) {
if (identical(oriGrid, newGrid, n)) {
cout << i + 1 << endl;
return 0;
}
rotate90(oriGrid, n);
}
horizontalReflection(oriGrid, n);
for (int i = 0; i < 4; ++i) {
if (identical(oriGrid, newGrid, n)) {
if (i > 0) i = 1;
cout << i + 4 << endl;
return 0;
}
rotate90(oriGrid, n);
}
if (identical(oriGrid, newGrid, n)) {
cout << 6 << endl;
return 0;
}
cout << 7 << endl;
return 0;
}
bool identical(string* a, string* b, int n) {
for (int i = 0; i < n; ++i) {
string strA = *a, strB = *b;
for (int j = 0; j < n; ++j) {
if (strA[j] != strB[j]) return false;
}
++a; ++b;
}
return true;
}
void rotate90(string* a, int n) {
for (int i = 0; i < n / 2; ++i) {
for (int j = i; j < n - i - 1; ++j) {
char temp = (*a)[j];
(*a)[j] = (*(a + (n - j - 1)))[i];
(*(a + (n - j - 1)))[i] = (*(a + (n - 1 - i)))[n - 1 - j];
(*(a + (n - 1 - i)))[n - 1 - j] = (*(a + j))[n - 1 - i];
(*(a + j))[n - 1 - i] = temp;
}
}
}
void horizontalReflection(string* a, int n) {
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n / 2; ++j) {
char temp = (*a)[j];
(*a)[j] = (*a)[n - j - 1];
(*a)[n - j - 1] = temp;
}
++a;
}
}
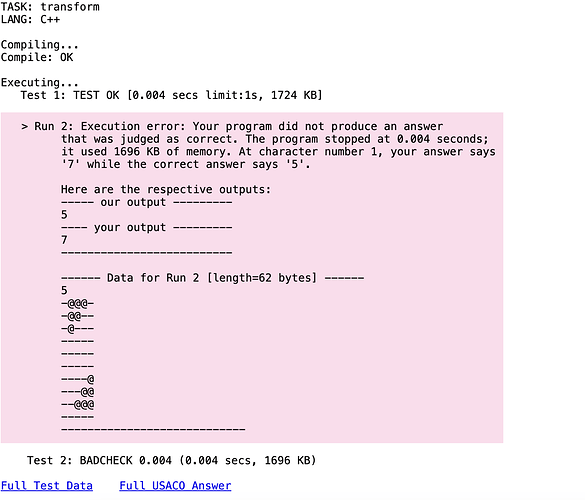
I believe that the described case is indeed impossible with the 6 described operations as the original pattern cannot be changed into the new one by rotation, horizontal reflection or those combined. Hence the result should be 7(impossible with given transformations). However, the stated correct output is 5(combination of transformations).
Therefore I come to a conclusion that I have understood the question incorrectly, but I am unable to find why.
Could anyone please explain to me my misinterpretation? Any help is very much appreciated. ![]()
![]()
![]()