Problem Info
The problem is called Camelot and can be found here.
Question
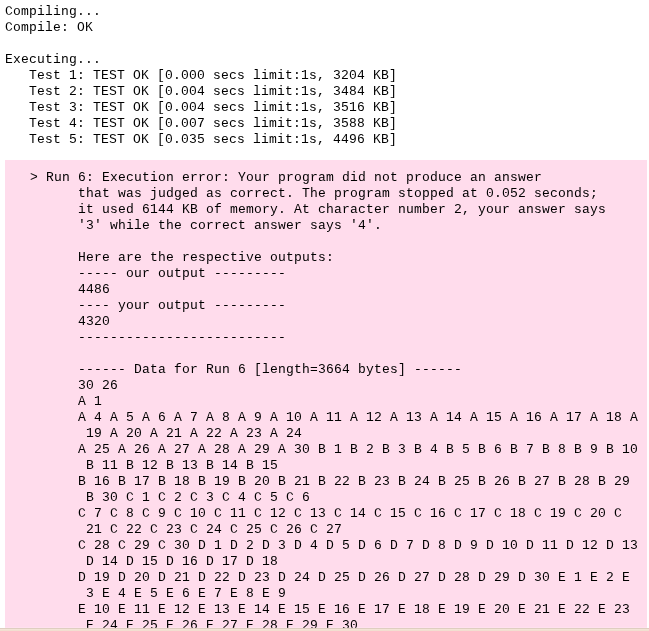
My code outputs the wrong answer for a test case and I have no idea why.
What I’ve Tried
I have downloaded the test data and tried it out, but it outputs the wrong answer. I have written another solution that is a bit more like brute force, but it outputs the same incorrect answer.
My Work
/*
ID: REDACTED
LANG: C++
TASK: camelot
*/
#include <iostream>
#include <vector>
#include <queue>
#include <cstdio>
#include <algorithm>
std::vector<std::vector<int>> make_neighbors(int rows, int cols) {
std::vector<std::vector<int>> moves = {{-1, -2}, {-2, -1}, {1, -2}, {-2, 1}, {2, -1}, {-1, 2}, {1, 2}, {2, 1}}, neighbors(rows * cols, std::vector<int>());
int new_row, new_col;
for (int row = 0; row < rows; row++) {
for (int col = 0; col < cols; col++) {
for (std::vector<int> move : moves) {
new_row = row + move[0];
new_col = col + move[1];
if (new_row >= 0 && new_row < rows && new_col >= 0 && new_col < cols) {
neighbors[row * cols + col].push_back(new_row * cols + new_col);
}
}
}
}
return neighbors;
}
std::vector<std::vector<int>> find_distances(int rows, int cols) {
std::vector<std::vector<int>> knight_distance(rows * cols, std::vector<int>(rows * cols, 1e6)), neighbors = make_neighbors(rows, cols);
std::queue<int> unsearched;
int distance, current;
for (int square = 0; square < rows * cols; square++) {
unsearched = std::queue<int>();
unsearched.push(square);
knight_distance[square][square] = 0;
while (unsearched.empty() == 0) {
current = unsearched.front();
distance = knight_distance[square][current];
unsearched.pop();
for (int next_position : neighbors[current]) {
if (knight_distance[square][next_position] == 1e6) {
unsearched.push(next_position);
knight_distance[square][next_position] = distance + 1;
}
}
}
}
return knight_distance;
}
int min_moves(int rows, int cols, std::vector<int> king, std::vector<std::vector<int>> knights) {
std::vector<std::vector<int>> knight_distance = find_distances(rows, cols);
int current_moves, knight_pos, total_moves = 1e6, extra_moves, king_distance, king_to_target, gather_square;
for (int target = 0; target < rows * cols; target++) {
king_to_target = std::max(std::abs(king[0] - target / cols), std::abs(king[1] - target % cols));
current_moves = 0;
extra_moves = 1e6;
for (std::vector<int> &knight : knights) {
current_moves += knight_distance[knight[0] * cols + knight[1]][target];
}
for (int gather_i = std::max(0, king[0] - 2); gather_i <= std::min(rows - 1, king[0] + 2); gather_i++) {
for (int gather_j = std::max(0, king[1] - 2); gather_j <= std::min(rows - 1, king[1] + 2); gather_j++) {
gather_square = gather_i * cols + gather_j;
king_distance = std::max(std::abs(king[0] - gather_i), std::abs(king[1] - gather_j));
for (std::vector<int> &knight : knights) {
knight_pos = knight[0] * cols + knight[1];
if (knight_distance[knight_pos][gather_square] + knight_distance[gather_square][target] - knight_distance[knight_pos][target] + king_distance < extra_moves) {
extra_moves = knight_distance[knight_pos][gather_square] + knight_distance[gather_square][target] - knight_distance[knight_pos][target] + king_distance;
}
}
}
}
extra_moves = std::min(extra_moves, king_to_target);
total_moves = std::min(total_moves, current_moves + extra_moves);
}
return total_moves;
}
int main() {
std::freopen("camelot.in", "r", stdin);
std::freopen("camelot.out", "w", stdout);
std::ios::sync_with_stdio(false);
std::cin.tie(0);
int rows, cols, row, col;
char letter_row;
std::cin >> rows >> cols;
std::vector<int> king;
std::cin >> letter_row >> col;
row = letter_row - 'A';
king = {row, col - 1};
std::vector<std::vector<int>> knights;
while (std::cin >> letter_row >> col) {
row = letter_row - 'A';
knights.push_back({row, col - 1});
}
int result = min_moves(rows, cols, king, knights);
std::cout << result << "\n";
return 0;
}
The code uses BFS to find the distance between two squares if you are traveling by a knight. Then, it loops through all possible squares where all the pieces could end. For each of these squares, it looks at if a knight and a king meet up at a square, and then move to the ending square would be better. I don’t think the issue is in restricting the intermediate squares which a knight and a king meet up, since unrestricting the squares doesn’t change the output.