Hello All,
I understand the solution to the problem, but I don’t quite understand why my solution doesn’t work.
I’ve tried this approach to another problem, War, but it also didn’t work so I would like to know why this approach generally fails.
For this problem, if we consider each color as a component, from the optimal construction of components, consider each component as a node. Then, we will have a collection of lines(ex: A->B->C and circles (ex: A->B->C->A), where each node can have at most outgoing edge and at most one incoming edge.
Then, we keep track of which component each component is connected to instead of keeping an adjacency list and merging two adjacency lists. Then, after two components are connected, we recursively connect the components pointing to those two components.
Here is my code which I think will give a better explanation.
import java.util.*;
import java.io.*;
public class FavoriteColors {
public static void main (String[] args) throws IOException {
//Kattio io = new Kattio("fcolor");
Kattio io = new Kattio();
int N = io.nextInt();
int M = io.nextInt();
UnionFind graph = new UnionFind(N);
//find all distinct colors
for (int m = 0; m<M; m++) {
//a points to j
int a = io.nextInt()-1;
int b = io.nextInt()-1;
graph.directedEdge(a,b);
}
//optimize number for each color
HashMap<Integer, Integer> used = new HashMap<>();
//io.println(Arrays.toString(graph.nodes));
for (int i = 0; i<N; i++) {
if (!used.keySet().contains(graph.find(i))) {
int s = used.keySet().size()+1;
io.println(s);
used.put(graph.find(i), s);
}
else {
io.println(used.get(graph.find(i)));
}
}
io.close();
}
public static class UnionFind {
int[] nodes;
int[] sizes;
int components;
int[] in;
UnionFind(int n) {
nodes = new int[n];
sizes = new int[n];
components = n;
in = new int[n]; // num[i] points to i
for (int i = 0; i < n; i++) {
nodes[i] = i;
sizes[i] = 1;
in[i] = -1;
}
}
void directedEdge (int a, int b) {
//there is a directed edge from a to b
if (a == -1 || b == -1) {
return;
}
int i = find(a);
int j = find(b);
//component i points to component j
int inJ = find(in[j]);
//need to unite i and the component pointing to j
if (inJ != i) {
union(i, inJ);
//update the component pointing to j for future use
in[find(j)] = find(i);
if (inJ != -1) {
//need to merge the components pointing to i and inJ
//do this by creating a directed edge from either in[inJ] or in[i] to the leader of (i, inJ)
if (find(i) == i) {
directedEdge(find(in[inJ]), i);
}
else { //find(i) = inJ
directedEdge(find(in[i]), inJ);
}
}
}
}
void union (int p, int q) {
if (p == -1 || q == -1) {
return;
}
int i = find(p);
int j = find(q);
if (i == j) return;
components--;
if (sizes[i] < sizes[j]) {
nodes[i] = nodes[j];
sizes[j] += sizes[i];
} else {
nodes[j] = nodes[i];
sizes[i] += sizes[j];
}
}
int find (int index) {
if (index == -1) {
return -1;
}
while (nodes[index] != index) {
nodes[index] = nodes[nodes[index]];
index = nodes[index];
}
return index;
}
}
//Kattio
public static class Kattio extends PrintWriter {
private BufferedReader r;
private StringTokenizer st;
// standard input
public Kattio() { this(System.in, System.out); }
public Kattio(InputStream i, OutputStream o) {
super(o);
r = new BufferedReader(new InputStreamReader(i));
}
// USACO-style file input
public Kattio(String problemName) throws IOException {
super(problemName + ".out");
r = new BufferedReader(new FileReader(problemName + ".in"));
}
// returns null if no more input
public String next() {
try {
while (st == null || !st.hasMoreTokens())
st = new StringTokenizer(r.readLine());
return st.nextToken();
} catch (Exception e) { }
return null;
}
public int nextInt() { return Integer.parseInt(next()); }
public double nextDouble() { return Double.parseDouble(next()); }
public long nextLong() { return Long.parseLong(next()); }
}
}
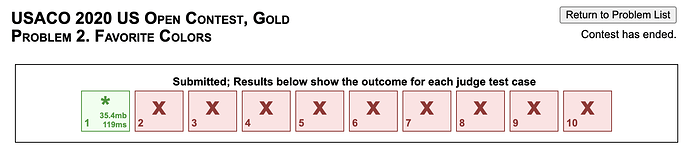
The code passes only the first test case.
I’ve tried debugging this, but after the first testcase, the size of the graph is too big to debug.
I’ve also tried using a random number generator to test a few small cases myself, but it seems to work fine.
Thank you!