Polynomial Hash (for 2d grid) Question

#1

USACO Problem: Bull in a China Shop

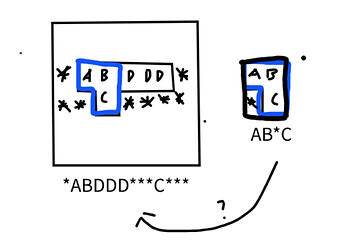
One part that I don’t get about this problem is how exactly hashing each piece allows us to “place” (aka subtract off) two pieces from the original piece. (For reference, here’s the part of the official solution referring to that)

The next piece of the puzzle is to use polynomial hashing to eliminate a O(k) factor on the critical path. After placing the first two pieces we can calculate the appropriate offset of the final piece and quickly test if its hash is one of the input pieces.

The issue is, calculating the hashes themselves doesn’t do any good because the pieces have different sizes. The hashes (written in string form) aren’t even comparable because the given dimensions end up truncating a bunch of (necessary) blank spaces.

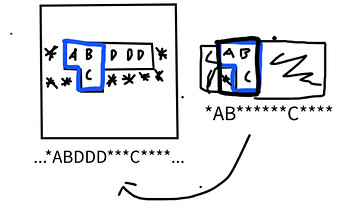
image
image1104×782 57.6 KB

I suppose you can add some padding to the piece and then compare them, but doing means that you have to calculate the hash for every grouping of pieces because the padding needed could possibly be different for each one.

image
image1186×744 71.5 KB

Offsetting the string (which is what the official code solution does) just pushes the entire substring along, which doesn’t fix the problem here. I’m not sure what I’m missing (but it might be kind of obvious since the solution never even mentions this issue lol). Any hints are appreciated. :slight_smile:

#2

I agree. This is not what the solution does though:

  void offset(int r, int c) {
    /* Offsetting the matrix by (r, c) translates into offsetting the
     * linearized array by r * MAXCOL + c.  Therefore we multiply each hash
     * by x^(r * MAXCOL + c). */
    for (int i = 0; i < HASHES; i++) {
      H[i] = (1ll * H[i] * POWTAB[i][r * MAXCOL + c]) % POLYMOD[i];
    }
  }

Essentially, it pads each row of the grid until they all have length MAXCOL.

#3

I see… It took me a while to realize that the hashes were originally generated like below:

image
image710×472 28.3 KB

Thanks for your help!