Introductory Dynamic Programming Problem

Problems and Contests
#1

Hi,

I am learning about dynamic programming. I have a basic idea of what it entails, but I am not clear how to go about memoizing a piece of recursive code I have wrote. The details are below.

In order to practice dynamic programming, I am working through the Atcoder educational DP contest here:

https://atcoder.jp/contests/dp/tasks

I am currently working through task: Frog 1. I want to solve this using recursion + memoization as opposed to tabulation to learn the concept.

Conceptual Solution

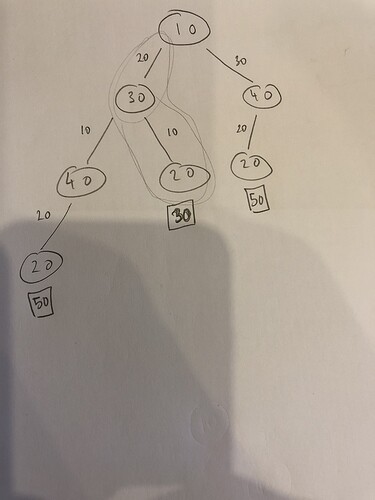
I visualise this as a tree. The left leg is the i + 1 node, whereas the right leg is the i + 2 node. The weight of the edge is the cost of moving to that node. For test case 1, here is how it looks (the optimal cost in the square boxes):

IMG_4931
IMG_49313024×4032 1.67 MB

Base case: If we are at the final stone (in this case 20), return the cost.The cost is shown in the square boxes in the picture.

Recursive case: At each stone we have two choices: move forward 1 or move forward 2. We are guaranteed to hit the final stone using a combination of the feasible steps from any node. I just have a bit of logic to pick the shortest path calculated from the current node to the destination node.

Code Solution

My attempt in code:

from sys import stdin
import math

fin = open("test.in")

N = int(fin.readline().strip())

stones = [int(x) for x in fin.readline().split()]

def traverse(i, stones, cost = 0):
    if i == N - 1: return cost

    a = None
    b = None

    if i + 1 < N:
        a = traverse(i + 1, stones, cost + abs(stones[i] - stones[i + 1]))
    
    if i + 2 < N:
        b = traverse(i + 2, stones, cost + abs(stones[i] - stones[i + 2]))

    if a is not None and b is not None: return min(a, b)
    if a is None and b is not None: return b
    if a is not None and b is None: return a
    
print(traverse(0, stones))

This seems to work and give the correct answer.

Now my problem is I do not know how to memoize this. I can see there are overlapping subproblems and I am doing repeated work, so it is possible to memoize. Could someone skilled at this please give me a hint as to how to approach memoizing my code.

#2

Right now, there’s only 1 parameter that you need for the recurrence, and that’s the location you’re at. Don’t you think you could somehow cache this result and spit it back whenever it’s needed again?

Also, on a side note, recursion isn’t that often used for dynamic programming. I suggest you look into using something called a DP array instead.

1 Like
#3

Thanks - I restructured my code and memoized it using the tips you gave.

I guess I just need to keep practicing - I do find this topic pretty challenging vs the others I’ve seen.

#4

Yeah, I found it really challenging as well. And yeah, the only way to get better is to keep practicing- eventually you’ll start to feel it in your bones.