Problem here:
http://www.usaco.org/index.php?page=viewproblem2&cpid=714
I read the given solution here:
http://www.usaco.org/current/data/sol_helpcross_silver_feb17.html
And I’m trying to understand its correctness.
So here’s what I’ve come up with. Suppose we run the algorithm and then suppose this is not a maximal result, and then show a proof by contradiction.
An “unmatched cow” is a cow that has not been matched with any chicken in the final result. So if this is not maximal, there must be at least unmatched cow that could have been matched with a chicken.
Could it still be possible after running the algorithm to pick a single chicken and a single
cow and match them? But the algorithm would have found that chicken when it first ran.
The other way we can have an unmatched cow U is that at least one matched cow M has a choice of chickens, H1 and H2. In the algorithm we chose a chicken H1 that could have also been matched with U, and then H2 is not within the time range of U so we don’t have the option to match U. We lost the opportunity by choosing wrong with M.
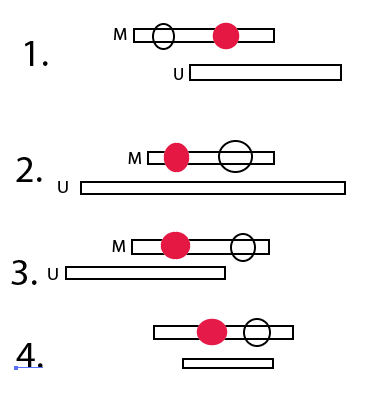
The four cases in the diagram show the four ways that U can overlap with M, given different lengths and positions of U.
In the diagram, case 1 shows M with the two chickens as circles superimposed. The red one is the one we chose to match with M and we can see how in an optimal result we would choose the other chicken to match with M. But this scenario contradicts the algorithm, which is that it would have chosen the earlier chicken to match with M.
Case 2 is also a contradiction because it would leave an unmatched chicken that would have been picked up the first time the algorithm ran.
Case 3 is a contradiction: it would have matched the earlier red chicken with U first, because U ends earlier than M.
Case 4 is similar to case 2.
Let me know if I’m track here or if there is some simpler way to express this.